Adinkras

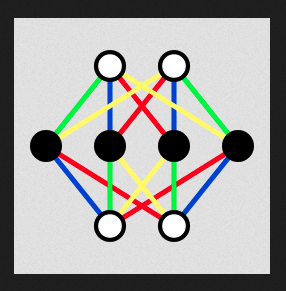
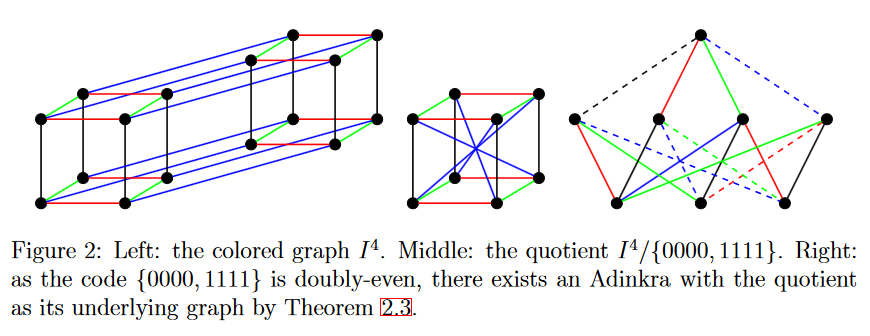
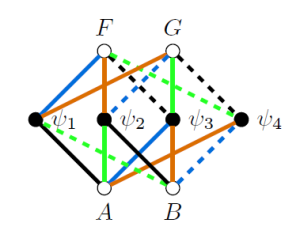
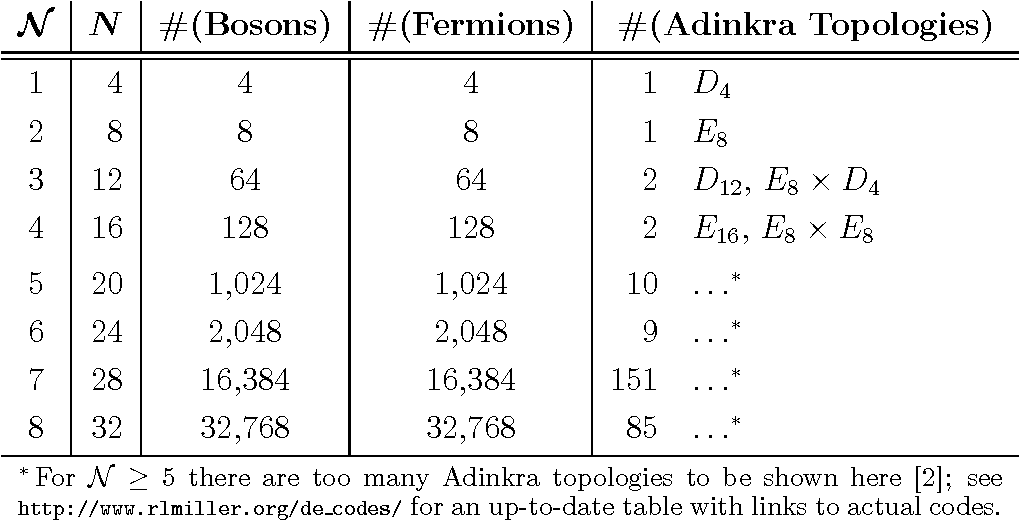
Definition

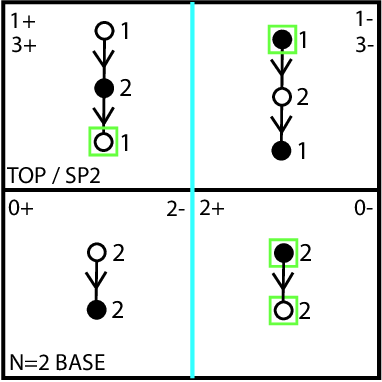
Adinkras are graphical representations used in theoretical physics, particularly in the study of supersymmetry. They visually depict the symmetry transformations and field properties of particles in supersymmetric theories. Filled vertices represent even fields (e.g., bosons), while open vertices represent odd fields (e.g., fermions). Arrows between vertices show how these fields transform under supersymmetry. Adinkras help physicists analyze the complex symmetries and particle representations in supersymmetric theories, aiding in our understanding of fundamental physics principles.

Quantum Physics – Superfields, Supergravity and Supersymmetry

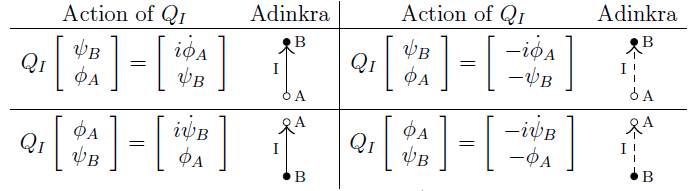
Symbols

Symbol	Definition
•	Filled vertex in Adinkra representing an even field.
∘	Open vertex in Adinkra representing an odd field.
{}	Curly braces used for grouping elements or concepts.
∼	Symbol representing a connection or transition.
→	Directed arrow in Adinkra indicating a transformation.
↓↙↘	Arrows with different directions signifying transformations.
↪	Arrow indicating inclusion or embedding into another structure.
⇒	Symbol representing an implication or logical connection.
↔	Bidirectional arrow indicating a reversible transformation.
↦	Arrow representing a mapping or transformation.
∝	Signifying proportionality or a mathematical relationship.
∂	Symbol for a partial derivative in calculus.
𝝊	Represents a smooth flow or vector field on a smooth space.
pt	Likely represents a point or a specific mathematical object.
p	Mapping or function.
Obj()	Set of objects in a category.
End()	Endomorphism of an object in a category.
𝚪	Functor or mathematical operator linking structures.
ℝ	Set of real numbers.
ℤ	Set of integers.
⊗	Tensor product for combining vector spaces.
Q	Set of rational numbers.
T	Tangent space or transformation.
C	Set of complex numbers.
N	Supersymmetry parameter, indicating supersymmetry generators.
n, m	Indices used for components or elements within structures.
t	Symbol for time in physical theories.
i	Imaginary unit (square root of -1).
d	Represents a differential or small change in a variable.
ϕ	Greek letter commonly used for variables or fields.
ψ	Greek letter often used to represent wave functions or quantum states.

Details

1. •: This symbol represents a filled vertex in an Adinkra diagram. It typically corresponds to an even (bosonic) field in the supersymmetric theory.
2. ∘: This symbol represents an open vertex in an Adinkra diagram. It typically corresponds to an odd (fermionic) field in the supersymmetric theory.
3. {}: Curly braces are used to group elements or concepts together, such as specifying the structure of a fat point or a set of transformations.
4. ∼: This symbol appears to represent a connection or transition between different elements in an Adinkra diagram, possibly indicating a transformation or relationship between fields.
5. →: This arrow symbol represents a directed arrow in an Adinkra diagram, indicating a transformation or connection between fields or vertices.
6. ↓↙↘: These arrow symbols with different directions represent various transformations or connections between fields in an Adinkra diagram. The specific meaning would depend on the context of the diagram.
7. ↪: This arrow symbol indicates an inclusion or embedding of one mathematical structure into another, such as embedding a fat point into a categorical tangent bundle.
8. ⇒: This symbol represents an implication or logical connection between mathematical concepts or statements.
9. ↔: This symbol represents a bidirectional arrow, typically indicating a reversible transformation or relationship between mathematical objects.
10. ↦: This arrow symbol typically represents a mapping or transformation between mathematical objects, such as mapping from a fat point to the categorical tangent bundle.
11. ∝: This symbol indicates proportionality or a mathematical relationship between quantities.
12. ∂: This symbol represents a partial derivative in calculus, often used to describe changes or transformations in physical systems.
13. 𝝊: This symbol represents a smooth flow or vector field, particularly in the context of transformations on a smooth space.
14. pt: This likely represents a point or a mathematical object with specific properties, as mentioned in the context of fat points and superpoints.
15. p: In the context of “p: TC→Obj(C)∝,” it seems to represent a mapping or function.
16. Obj(): This likely represents the set of objects in a category, as used in the context of category theory.
17. End(): This may represent the endomorphism of an object in a category, which describes morphisms from an object to itself.
18. 𝚪: In the context of “𝚪(TC),” it may represent a functor or a mathematical operator that relates different mathematical structures.
19. ℝ, ℤ, ⊗, Q, T, C, N, n, m, t, i, d, ϕ, ψ: These symbols represent various mathematical constants, operators, and variables used in the formulas and equations described in the excerpt. Their meanings would depend on the specific equations and contexts in which they are used.

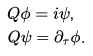
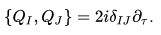
These symbols are integral to understanding the mathematical and graphical representations of supersymmetric theories, Adinkras, and related concepts in theoretical physics.

1. ℝ (Real Numbers):
   • ℝ represents the set of real numbers, which includes all the numbers on the real number line. It is often used to describe quantities with continuous values in mathematical and physical contexts.
2. ℤ (Integers):
   • ℤ represents the set of integers, which includes all positive and negative whole numbers, as well as zero. In some contexts, it might be used to label discrete quantities or indices.
3. ⊗ (Tensor Product):
   • ⊗ represents the tensor product, a mathematical operation used to combine vector spaces or tensors. In the context of n-categories, it’s used to define the tensor product of n-categories, leading to a new n-category.
4. Q (Rational Numbers):
   • Q represents the set of rational numbers, which includes all numbers that can be expressed as a ratio of two integers. It’s often used in mathematical calculations and represents fractions.
5. T (Tangent):
   • T is used in the context of the categorical tangent bundle, which is a mathematical construct used in category theory to describe the tangent space of a category. It’s related to understanding transformations or changes within the category.
6. C (Complex Numbers):
   • C represents the set of complex numbers, which includes real and imaginary parts. Complex numbers are used extensively in quantum mechanics and other areas of physics to represent physical quantities.
7. N (Supersymmetry Parameter):
   • N is used to represent the supersymmetry parameter in the context of N-extended supersymmetry. It indicates the number of supersymmetry generators and is a fundamental parameter in supersymmetric theories.
8. n, m (Indices):
   • n and m are commonly used as indices in mathematical expressions to denote specific components or elements within a larger structure, such as arrays or matrices.
9. t (Time):
   • t often represents time in physical theories, particularly in the context of dynamics and transformations. It’s a fundamental parameter in many physics equations.
10. i (Imaginary Unit):
    • i represents the imaginary unit, defined as the square root of -1. It’s used in complex numbers and various mathematical operations, such as rotations in the complex plane.
11. d (Differential):
    • d is often used in calculus to represent a differential or a small change in a variable. It’s crucial for describing derivatives and integrals in mathematical expressions.
12. ϕ (Phi):
    • ϕ is a Greek letter commonly used to represent a variable or field in mathematical and scientific equations. Its specific meaning would depend on the context of the formula.
13. ψ (Psi):
    • ψ is another Greek letter used to represent a variable or field in mathematical and scientific equations. It’s often used in quantum mechanics to represent wave functions or quantum states.

African Adinkras and Quantum Physics

A Cultural Symbology Perspective

Adinkras, whether from African culture or quantum physics mathematics, represent more than meets the eye. This exploration unveils intriguing parallels between these seemingly distant worlds, shedding light on their cultural and mathematical significance.

African Adinkras: Cultural Symbology

Origin and Tradition: African Adinkras hail from the Akan people of Ghana and Cote d’Ivoire, embodying profound cultural and philosophical meanings.

Visual Language: These symbols form a visual language, conveying complex ideas, proverbs, and values, making them a rich repository of cultural wisdom.

Unity of Opposites: Many Adinkras symbolize “Sankofa,” encapsulating the unity of opposites and the idea of learning from the past while moving forward, a theme also found in quantum physics.

Quantum Physics Adinkras: Mathematical Abstraction

Supersymmetry and Lie Superalgebras: In quantum physics, Adinkras serve as a mathematical tool to represent Lie superalgebras, notably in the context of supersymmetry. They unite fermions and bosons, akin to African Adinkras uniting opposing elements.

Representation Theory: Adinkras facilitate the study of representations of supersymmetry algebras, using filled and open vertices to depict even (bosonic) and odd (fermionic) fields, mirroring African Adinkras’ unity of opposites.

Bridging the Abstract and the Concrete: Adinkras bridge the gap between abstract mathematics and tangible physics, visually illustrating complex symmetries and transformations, reminiscent of African Adinkras’ communication of cultural concepts.

Parallels and Convergence

Unity of Opposites: Both African Adinkras and Quantum Physics Adinkras embody the unity of opposites, whether in cultural wisdom or quantum symmetries.

Symbolic Language: Both Adinkra sets are symbolic languages conveying profound ideas, be it cultural values or mathematical relationships.

Deep Philosophical Roots: Rooted in deep philosophy, African Adinkras and Quantum Physics Adinkras emphasize interconnectedness, uniting cultural symbolism and mathematical abstraction.

Conclusion

African Adinkras and Quantum Physics Adinkras, though from distinct realms, share threads of unity, symbolism, and profound philosophy. They remind us that the quest for understanding transcends boundaries, offering insights into the rich tapestry of human knowledge and creativity.